Avant de nous lancer dans l’aventure de la recherche d’une particule, une petite introspection dans la théorie de ce domaine de la physique est inévitable : on ne peut pas chercher efficacement une particule sans en connaître les propriétés, comme on ne va pas chercher un livre dans une bibliothèque sans en connaître le titre, l’auteur et/ou la couleur de la couverture.

Plan de ce chapitre

• Plan de ce chapitre
• La physique des particules, qu’est-ce que c’est ?
• Structure de la matière
• Le Modèle Standard de la physique des particules
  • La matière
  • Les forces ou interactions
  • Les propriétés des particules
  • Les propriétés des interactions
    • Le confinement
    • Conséquence expérimentale
    • Une vision plus réaliste du proton
  • Diagrammes de Feynman
• Le problème de la masse et sa solution

La physique des particules, qu’est-ce que c’est ?

Rentrons dans le vif du sujet : un physicien des particules cherche à comprendre de quoi est faite la matière qui nous entoure à son niveau le plus fondamental, et comment les différents éléments qui la constituent interagissent entre eux. La technique utilisée jusqu’à maintenant, avec succès, a été de creuser ou plutôt de regarder de plus en plus près. De la même manière qu’en s’approchant d’un tableau pointilliste, on en voit les détails et on peut admirer la technique de l’artiste¹, la matière se révèle quand on regarde dans l’infiniment petit. Commençons donc notre descente dans les entrailles de la matière.

Structure de la matière

Commençons donc notre plongée au cœur de la matière. Le modèle que je vais vous montrer est la vision actuelle de la structure de la matière, celle-ci ayant beaucoup évoluée avec le temps. L’objectif ici est juste de décrire le tableau, pas tous les traits de pinceaux qui ont permis de l’obtenir.

Avant tout, un petit rappel des échelles de longueurs auxquelles on va travailler : la figure suivante classe quelques objets que vous reconnaîtrez sur un axe gradué en longueur.

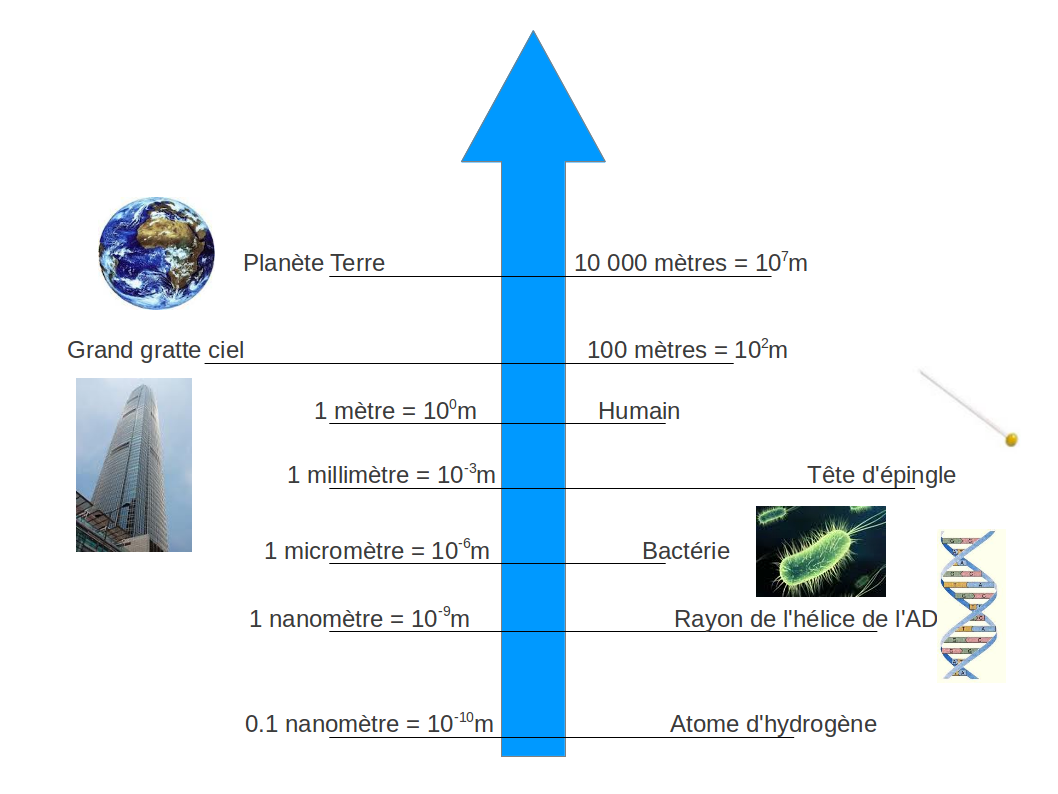
Notre point de départ sera l’atome, déjà plus petit que le nanomètre, constituant électriquement neutre de tous les matériaux de la vie courante, mais aussi du Soleil et de toutes les autres étoiles, et même de tous les objets célestes. L’atome n’est pas “élémentaire” dans le sens où on lui connaît une structure interne : on peut le décomposer en un noyau, positif, autour duquel gravitent des électrons, négatifs.

En ce qui concerne l’électron, aucune structure interne n’a été découverte jusqu’à maintenant. Pour nous, l’électron est donc une particule élémentaire.

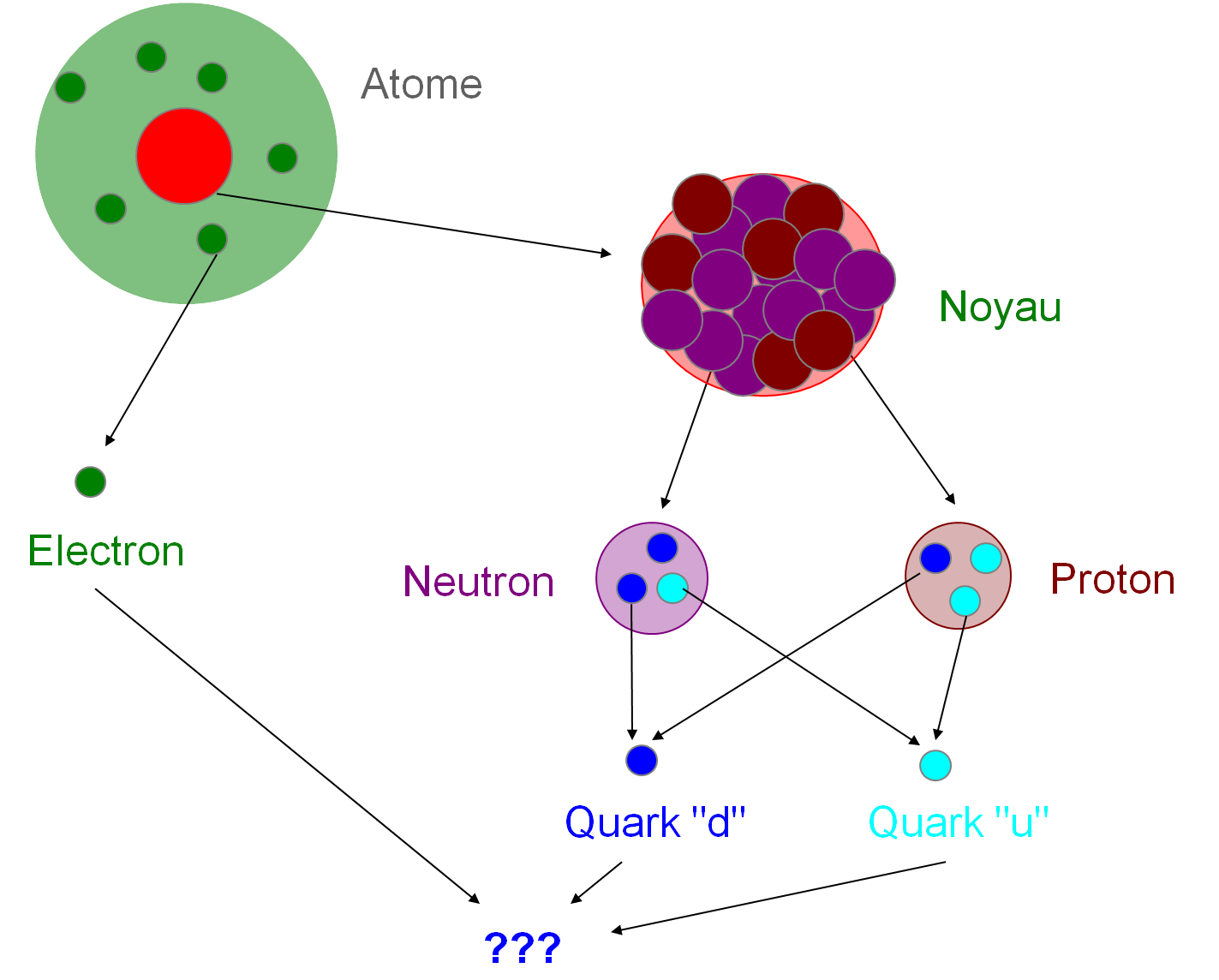
En revanche, l’histoire n’est pas la même pour le noyau atomique : il a été montré qu’il était principalement formé de deux types d’objets : les protons, de charge électrique positive, et les neutrons, qui, comme leur nom l’indique, sont électriquement neutres, c’est-à-dire que leur charge électrique est nulle. Les protons et les neutrons sont l’objet d’étude de la physique nucléaire. La physique des particules s’occupe d’objets encore plus petits. Parce que les protons et les neutrons ont encore une structure interne : ils sont formés de particules qu’on appelle “quarks” et qui sont considérés aujourd’hui comme élémentaires au même titre que les électrons (mais peut-être n’avons nous juste pas encore inventé le bon instrument pour révéler cette composition ?).

Il existe différents types de quarks, qui peuvent se regrouper pour former des particules plus grosses. Par exemple, le protons et le neutrons sont formés chacun de 3 quarks : deux quarks u et un quark d pour le proton; un quark u et deux quarks d pour le neutron.

Ces trois particules élémentaires (électron, quark u et quark d) nous permettent de commencer à construire le Modèle Standard de la physique des particules.

Le Modèle Standard de la physique des particules

La matière

À ces trois particules, il faut ajouter une quatrième : le neutrino électronique, particule neutre et très légère, introduite de manière théorique pour assurer la conservation de l’énergie dans certaines réactions et découverte expérimentalement quelques années plus tard.

L’histoire des neutrinos est un bel exemple de complémentarité entre théorie et expérience en physique. Je vous en parlerai peut-être plus tard pour ne pas trop m’éparpiller ici.

Ces quatre particules élémentaires donc forment ce qu’on appelle la première famille de particules élémentaires qui constitue la matière de tous les jours. Le tableau ci-dessous présente les différentes particules élémentaires. Les chiffres entre parenthèse sont les charges électriques ²: on reconnaît le -1 pour l’électron et le 0 pour le neutrino. Par contre les quarks ont des charges électriques assez inhabituelles car fractionnaires.

Comme vous pouvez le voir sur la figure précédente, les quatre particules qu’on a vu forment la première famille de particules élémentaires. Mais beaucoup d’autres ont été découvertes dans la suite, en observant les rayons cosmiques par exemple, et ont pu être classées dans deux nouvelles familles, qui contiennent des particules aux propriétés semblables à celles de la première famille, mais plus lourdes. Par exemple, le muon est le “cousin” de l’électron, de même charge électrique, mais avec une masse plus élevée.

On arrive donc à un total de douze particules élémentaires. Et c’est tout. Ou presque…

Ceci achève notre description actuelle de la matière : un total de 24 particules.

Vous pensez qu’on a fini ? Et bien non, il nous manque encore un élément indispensable : comprendre comment toutes ces particules interagissent entre elles ? Qu’est-ce qui les les quarks dans le noyau par exemple ?

Les forces ou interactions

Pour répondre à cette question, on va faire la liste des interactions entre les particules en essayant de comprendre leur rôle.

• Une interaction que vous connaissez déjà et à laquelle je fais référence depuis le début de ce chapitre est l’interaction électrique, ou plus exactement électromagnétique. C’est elle qui agit sur les particules chargées, de sorte que… les opposés s’attirent et les contraires se repoussent. Ça vous rappelle quelque chose ?

• Si vous avez tout suivi, vous pouvez vous rendre compte que, si on ne considère que l’interaction électromagnétique, on a un problème… Rappelez-vous de la composition du noyau atomique : des protons de charge positive, qui vont donc se repousser par interaction électromagnétique, et des neutrons, qui ne subissent pas l’électromagnétisme. Comment alors peuvent-ils tenir ensemble dans un noyau ? La seule solution est d’introduire une nouvelle interaction, qui va au contraire de l’électromagnétisme, lier les protons et les neutrons. C’est l’interaction forte;

• Une autre interaction est nécessaire pour expliquer certaines radioactivités (des noyaux qui se cassent) : l’interaction faible;

• On sait qu’il existe une dernière interaction : la gravité. Cependant, personne n’est encore arrivé à l’inclure dans notre théorie pour le moment. Ce n’est pas “grave” dans le sens où elle a une intensité beaucoup plus faible que les trois interactions précédentes et peut donc être négligée sans que cela ait dimpact sur les expériences.

Notre construction du Modèle Standard est maintenant presque terminée. Il me reste un tout dernier point à vous présenter. Qui peut répondre à cette simple question : comment agissent les forces ? Plus précisément, comment une particule sait qu’il y a une autre particule à quelques centimètres d’elle ?

La physique des particules répond à cette question en imaginant un échange de particules médiatrices, encore appelées bosons, entre les particules qui subissent l’interaction. Le tableau ci-dessous montre les bosons associés à chaque intéraction :

Les propriétés des particules

Pour caractériser la matière, on doit déterminer quelles sont les propriétés qui la caractérise. Vous en connaissez déjà une : la charge électrique, qui détermine si une particule est ou nom sensible à la force électromagnétique. Mais il en existe d’autres. En voici une liste non exhaustive³ :

• La masse. L’unité de masse commune est le gramme (symbole : g). Cependant, les particules étant vraiment très légères, une autre unité à été introduite : l’électron-volt (symbole : eV). Pour effectuer la conversion, sachez que $0.5 MeV \approx 10^{-30} kg$;

• Le spin est une propriété strictement quantique. Je n’en ai pas parlé jusqu’à maintenant, mais les particules sont décrites par la mécanique quantique, qui a des propriétés assez inhabituelles parce que sans équivalent à notre échelle. Le spin en fait partie. L’image qu’on donne habituellement est celle d’une rotation.

Différences entre fermions et bosons : la figure suivante montre la répartition en énergie d’un système de plusieurs particules.

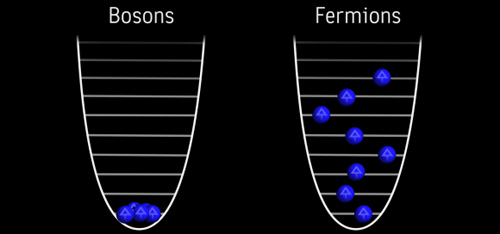
Deux fermions ne peuvent pas être dans le même état au même endroit : c’est la raison de la non-pénétrabilité de la matière. En revanche, deux bosons peuvent se regrouper dans le même état : cela est utile pour les forces qui sont plus ou moins intenses.

Les propriétés des interactions

Les interactions ont également leurs propriétés, qui peuvent, en général, être directement reliées aux caractéristiques de leur(s) boson(s) médiateur(s).

La portée d’une interaction caractérise la distance jusqu’à laquelle elle peut être ressentie. Par exemple, si je mets un aimant sur mon bureau, jusqu’à quelle distance les trombones seront attirés vers lui ? La distance à partir de laquelle les trombones ne réagissent plus est la portée de l’aimant. Cette propriété est corrélée à la masse des particules médiatrices : plus cette dernière est lourde, plus elle a du mal à aller loin et donc plus la portée de l’interaction sera courte.

Le confinement

Les quarks en particulier ont une proprété étrange : un quarks libre; cest-à-dire seul et loin des autres, n’exste pas ! C’est une conséquence de l’intensité de l’interacrtion forte, qui doit être suffisament forte pour vaincre la répulsion électromagnétique.

Imaginer une particule formée simplement de deux quarks. Si on veut séparer ces deux quarks, il faut tirer. Tirons donc, de plus en plus fort comme illustré sur la figure suivante. On apporte de l’énergie en tirant, mais cele ne suffit pas à vaincre l’interaction forte. A un certain point, l’énergie apportée sera suffisante pour former une nouvelle paire de particules, et d’une particule initiale formée de deux quarks, on arrive à deux particules finales, formées elles aussi de deux quarks. Mais on na pas réussi à obtenir un seul quarks libre…

Conséquence expérimentale

Ce dernier fait a une conséquence expérimentale forte. A votre avis, sous quelle forme alors apparaissent les quarks expérimentalement ? Comme ils ne sont pas observables seuls, isolés, ils apparaissent sous la forme de ce qu’on appelle dans le jargon “un jet” (à pronnoncer à l’anglo-saxonne), c’ést-à-dire un faisceau de particules (quarks) s’orientant dans la même direction :

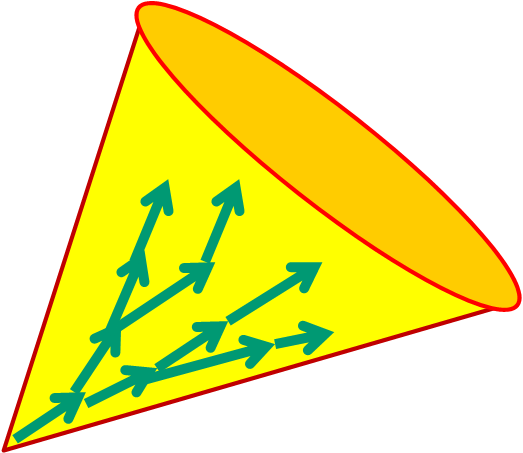
C’est une trace expérimentale fondamentalement différente des autres particules, mais nous y reviendrons.

Une vision plus réaliste du proton

On a vu un peu plus tôt que le proton est formé de trois quarks : deux $u$ et un $d$. Mais ces quarks doivent être liés pour tenir dans le proton. Cela veut dire quils échangent en permanence des gluons entre eux, gluons qui peuvent donner naissance à des quarks pour une courte durée. En réalité, un proton ressemblera plutôt à ceci :

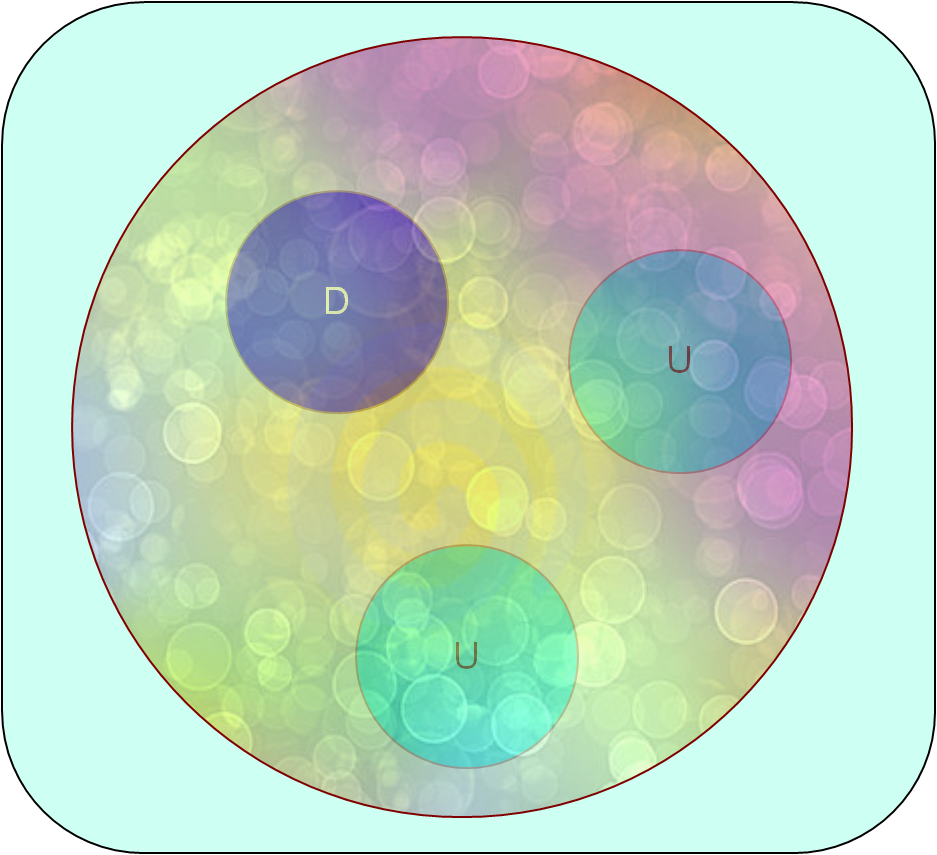
c’est-à-dire une soupe de quarks et de gluons, apparaissant et disparaissant sans cesse. C’est seulement si on prend une photo avec un temps d’exposition suffisamment long qu’on verra persister nos trois quarks.

Diagrammes de Feynman

Pour simplifier l’écriture des réactions qui peuvent se produire entre particules, les physiciens utilisent une notation spécifique, comme les chimistes le font pour les réactions chimiques. Il s’agit ici de ce qu’on appelle les diagrammes de Feynman, dans lesquels chaque particules est représentée par un type de ligne particulier. Les fermions sont généralement représentés par une ligne continue classique et les bosons par une ligne stylisée :

Force	Médiateur	Représentation
Electromagnétique	Photon
Forte	Gluon
Faible	W et Z

Le problème de la masse et sa solution

Nous en venons à parler du problème qui nous intéresse : la masse des particules. Dans un premier temps, laissez moi vous montrer quelles sont les masses mesurées des différentes particules élémentaires :

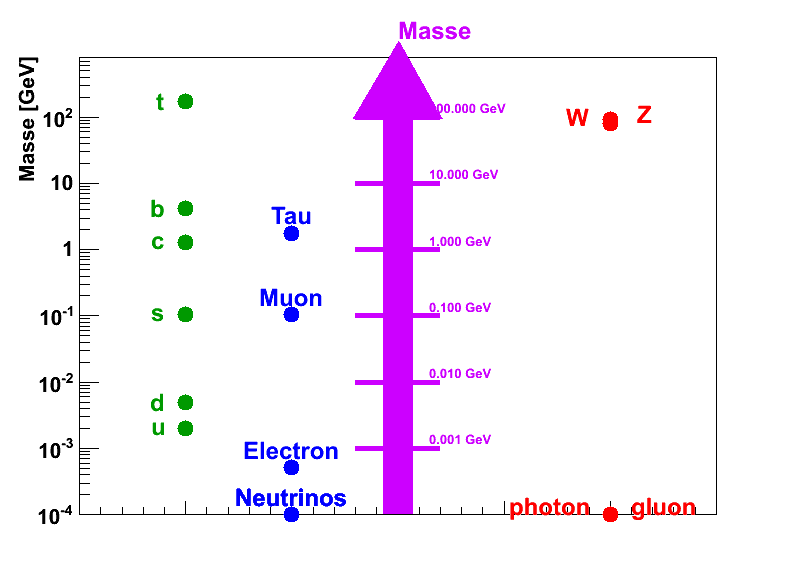
Les gluons ont une masse nulle, les photons également. Les neutrinos sont un cas un peu particulier : on a pensé pendant longtemps qu’ils étaient sans masse, mais de récentes expériences semblent monter qu’ils ont une masse, très faible cependant. On les considérera sans masse pour notre propos.

Les masses des particules massives sont donc très diverses : de 0.5 GeV pour l’électron à plusieurs centaines de GeV (un million de fois plus grand !). C’est un problème que l’on connais sous le nom de “mass hierarchy” ou hiérarchie des masses : pourquoi est-ce que les masses sont si différentes ? Cette question n’a pas de réponse approuvée expérimentalement à l’heure actuelle.

Bien, nous avons nos particules, nos forces, nos masses, il est où le problème ?

Le problème est le suivant : il se trouve que quand on essaye de créer une théorie mathématique à partir de toutes ces observations et de construire des équations, on n’arrive pas à expliquer pourquoi les bosons W et Z en particulier ont une masse. Ce qui est un peu embêtant sachant que les expériences leur trouvent des masses parmi les plus grandes mesurées pour des particules élémentaires…

La théorie est restée dans cet état jusque dans les années 60. Plusieurs physiciens se sont alors succédés pour bâtir petit à petit un modèle permettant enfin de générer des masses pour nos bosons. On retient en général trois noms pour cette idée, ceux de Brout, Englert et Higgs. Le mécanisme que nous nommerons par le suite mécanisme de BEH ou de Higgs pour simplifier vient d’une idée relativement simple (mais il fallait y penser) : supposons que ce qu’on appelle “vide” soit en réalité rempli de “quelque chose” qui va interagir avec les particules et les ralentir, un peu comme lorsqu’on essaye de marcher dans l’eau. Ce “quelque chose” est appelé par les physiciens “champ de Higgs”.

Comme dit plus haut, les particules vont interagir avec ce champ, et qui dit interaction en physique des particules dit particule associée à cette interaction ! C’est de là que vient le fameux boson de Higgs (j’oublie ici Brout et Englert, la paternité du boson est discutée, mais le consensus pour le moment et de dire que Higgs a été le premier a supposé l’existence d’une nouvelle particule).

Mais revenons à notre problème de masse. Comment l’introduction de ce champ ou de ces bosons permet de le résoudre ? Là encore je vais utiliser une image, illustrée sur la figure suivante. Imaginer une salle pleine d’une foule de fans. Soudain, la célébrité tant attendue, disons Brad Pitt, entre dans la pièce. Instantanément, on peut imaginer que les gens vont se regrouper autour de lui et ralentir sa progression. Et bien dans cette image, la foule représente le champ de Higgs, chacun des individu de cette foule est un boson de Higgs, et la célébrité est la particule qui acquiert une masse, un boson W par exemple.

Cette analogie nous permet d’aller plus loin, et de comprendre pourquoi les particules n’ont pas toutes la même masse. En effet, imaginer maintenant qu’au lieu de Brat Pitt, ce soit quelqu’un de moins célèbre, disons moi, qui fasse son entrée. N’étant pas connue, il est peu probable que des gens s’agglutinent autour de moi (je trouverais ça louche de toute façon). Je serai donc moins ralentie et, dans le monde de la physique des particules, j’aurais une masse plus faible. En physique, on ne parlera pas de degré de célébrité mais de couplage : plus une particule interagit avec le champ de Higgs, plus son couplage est fort et plus sa masse sera élevée.

On comprends maintenant pourquoi les particules ont une masse, et comment ces masses peuvent être si différentes.

Cette théorie est une solution élégante au problème de la masse, d’autant plus qu’elle prédit toutes les propriétés de cette nouvelle particule, hormis sa masse. Il reste tout de même un inconvénient, et pas des moindres : où est le boson de Higgs ? Je n’en ai pas parlé dans ma liste des particules élémentaires ? Et bien pendant très longtemps, jusqu’à l’été 2012 en fait, cette particule n’avait jamais été observée. Ce qui était un brin embêtant pour cette théorie et qui justifie le fait que sa découverte ait été un des objectifs principaux pour les physiciens des particules.

Après cette longue mais indispensable partie théorique, nous allons maintenant nous pencher sur les techniques expérimentales imaginées pour détecter les particules.